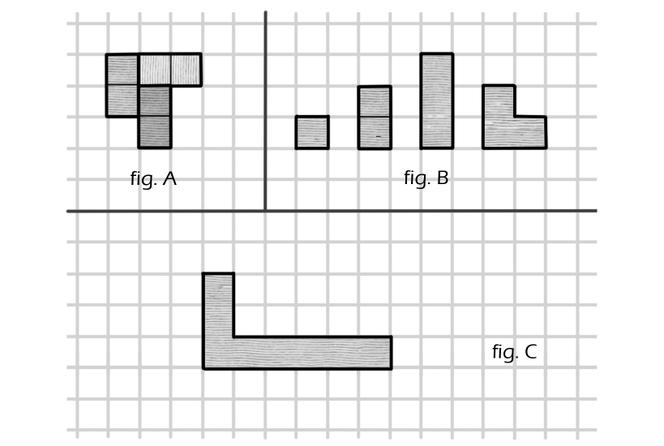
Il est facile de placer trois dominos de sorte que chacun touche les deux autres par un côté. La figure A en donne un exemple. En revanche, avec quatre dominos, quelle que soit la façon dont vous les poserez les uns à côté des autres, il y en aura toujours au moins deux qui ne seront pas en contact. Il est toutefois possible de trouver quatre formes qui peuvent toutes se toucher mutuellement. C’est le cas si on prend les quatre polyominos d’ordre inférieur ou égal à 3 : le monomino (qui n’est rien d’autre qu’un petit carré), un domino et les deux formes possibles de triominos, tous représentés sur la figure B.
Pouvez-vous placer ces quatre formes de façon que chacune touche les trois autres par au moins un côté ?
Notez que seuls les contacts le long des côtés sont autorisés et non seulement par un coin. De plus, les polyominos doivent rester dans le même plan, vous ne pouvez pas les superposer.
Se pose alors naturellement la question suivante : peut-on trouver un polyomino tel que quatre copies identiques (à rotations et symétries près) puissent toutes se toucher mutuellement ? La réponse est oui et le plus petit exemple possible est donné par l’octamino en L représenté sur la figure C.
Sauriez-vous trouver la configuration permettant à quatre de ces octaminos d’être tous en contact les uns avec les autres ?
Retrouvez les énigmes précédentes en cliquant ici
Contribuer



L’espace des contributions est réservé aux abonnés.
Abonnez-vous pour accéder à cet espace d’échange et contribuer à la discussion.